Post History

75%

+4 −0

Given a chess board with some knights on it, say how many squares are neither attacked by a knight nor containing a knight. Input An 8 by 8 grid where each square is either a knight or empty T...

3 answers · posted 2y ago by trichoplax‭ · last activity 1y ago by Karl Knechtel‭

Question code-golf

#9: Post edited by

trichoplax‭ · 2022-10-25T03:46:40Z (about 2 years ago)
Fix missing heading level in heirarchy

Copy Link

Raw

Markdown

Given a chess board with some knights on it, say how many squares are neither attacked by a knight nor containing a knight.
~~# Input~~
- An 8 by 8 grid where each square is either a knight or empty
- The input can contain any number of knights from 0 to 64
- You may choose to take input with any 2 distinct characters (or numbers or Booleans - there is no restriction to string input) representing a knight and an empty square
- You may take input in the format of your choice provided it does not provide additional information that would help solve the challenge
- For example, if you find it more convenient you could take input as a single 64 bit integer, where each bit is 1 for a knight and 0 for an empty square
~~# Output~~
- A number from 0 to 64, indicating the number of squares that satisfy both of:
- The square does not contain a knight
- The square is not a knight's move away from a knight.
A knight's move is either of:
- 2 squares horizontally (left or right) and 1 square vertically (up or down)
- 1 square horizontally (left or right) and 2 squares vertically (up or down)
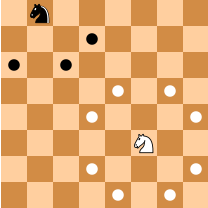[![Knight's moves shown as dots](https://codegolf.codidact.com/uploads/Q4kXyQDf3HZiX5NWncgRS2Fi)](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "View on Wikipedia")
(thanks to [Wikipedia](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "Wikipedia section on Knight's moves"))
~~# Example~~
The following example input has knights represented by `N` and empty squares represented by `*`.
```text
********
********
**N*****
********
********
********
******N*
N*******
```
Here it is again with attacked empty squares marked as `a`. The required output is the number of remaining squares (the number of squares still showing `*`).
```text
*a*a****
a***a***
**N*****
a***a***
*a*a*a*a
*a**a***
**a***N*
N***a***
```
So for this example, the output would be `47`.
~~# Test cases~~
### String input test cases
Test case inputs are given as 8 strings of 8 characters, followed by the output as an integer. Knights are represented by `N` and empty squares are represented by `*`.
```text
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
64
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
0
],
[
[
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
],
0
],
[
[
"N***N***",
"*N***N**",
"**N***N*",
"***N***N",
"N***N***",
"*N***N**",
"**N***N*",
"***N***N",
],
16
],
[
[
"N*******",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
61
],
[
[
"******N*",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
60
],
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"********",
"*****N**",
],
59
],
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"*N******",
"********",
],
59
],
[
[
"********",
"**N*****",
"********",
"********",
"********",
"********",
"********",
"********",
],
57
],
[
[
"********",
"********",
"**N*****",
"********",
"********",
"********",
"********",
"********",
],
55
],
[
[
"********",
"********",
"****N***",
"********",
"***N****",
"********",
"********",
"********",
],
48
],
[
[
"********",
"********",
"***N****",
"*****N**",
"**N*****",
"****N***",
"********",
"********",
],
36
],
[
[
"NNNNNNNN",
"NNN*N*NN",
"NN*NNN*N",
"NNNN*NNN",
"NN*NNN*N",
"NNN*N*NN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNNNN",
"NNN*N*NN",
"N***NN*N",
"*NNN*NNN",
"NN*NNN*N",
"*NN***NN",
"N*N*NNNN",
"NNNNNNNN",
],
2
],
[
[
"*NNNNNNN",
"NN*NNNNN",
"N*NNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNN*N",
"NNNN*NNN",
"NNNNN*N*",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNN*N*N",
"NNN*NNN*",
"NNNNN*NN",
],
1
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"*N*NNNNN",
"NNN*NNNN",
"N*NNNNNN",
"NNN*NNNN",
],
1
],
[
[
"*NNN*NNN",
"NN*NNNNN",
"*NNN*NNN",
"N*N*NNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"N*N*NNNN",
"*NNN*NNN",
"NN*NNNNN",
"*NNN*NNN",
"N*N*NNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"********",
"********",
"**N*****",
"********",
"********",
"********",
"******N*",
"N*******",
],
47
]
```
### Integer input test cases
If you choose to take input as a 64 bit unsigned integer, with each square being represented by a single bit, these are the equivalent of the test cases shown above, but with integer input.
Input which treats `1` bits as knights will be called ***one_knight_input***, and input which treats `0` bits as knights will be called ***zero_knight_input***. Since both of these are valid input types, both are included in the test cases so you can choose which to use.
Each test case is in the format `one_knight_input : zero_knight_input : output`.
```text
0 : 18446744073709551615 : 64
18446744073709551615 : 0 : 0
12273903644374837845 : 6172840429334713770 : 0
9819010546270478865 : 8627733527439072750 : 16
9223372036854775808 : 9223372036854775807 : 61
144115188075855872 : 18302628885633695743 : 60
4 : 18446744073709551611 : 59
16384 : 18446744073709535231 : 59
9007199254740992 : 18437736874454810623 : 57
35184372088832 : 18446708889337462783 : 55
8796361457664 : 18446735277348093951 : 48
17609903308800 : 18446726463806242815 : 36
18441077155848519679 : 5666917861031936 : 1
18440988645153550335 : 5755428556001280 : 2
9214294468855857151 : 9232449604853694464 : 1
18300371588261871615 : 146372485447680000 : 1
18446744073708891899 : 659716 : 1
18446744071024132079 : 2685419536 : 1
8637754208117850111 : 9808989865591701504 : 1
12643820184012849151 : 5802923889696702464 : 1
35184372089472 : 18446708889337462143 : 47
```
> Explanations are optional, but I'm more likely to upvote answers that have one.

Given a chess board with some knights on it, say how many squares are neither attacked by a knight nor containing a knight.
## Input
- An 8 by 8 grid where each square is either a knight or empty
- The input can contain any number of knights from 0 to 64
- You may choose to take input with any 2 distinct characters (or numbers or Booleans - there is no restriction to string input) representing a knight and an empty square
- You may take input in the format of your choice provided it does not provide additional information that would help solve the challenge
- For example, if you find it more convenient you could take input as a single 64 bit integer, where each bit is 1 for a knight and 0 for an empty square
## Output
- A number from 0 to 64, indicating the number of squares that satisfy both of:
- The square does not contain a knight
- The square is not a knight's move away from a knight.
A knight's move is either of:
- 2 squares horizontally (left or right) and 1 square vertically (up or down)
- 1 square horizontally (left or right) and 2 squares vertically (up or down)
[![Knight's moves shown as dots](https://codegolf.codidact.com/uploads/Q4kXyQDf3HZiX5NWncgRS2Fi)](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "View on Wikipedia")
(thanks to [Wikipedia](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "Wikipedia section on Knight's moves"))
## Example
The following example input has knights represented by `N` and empty squares represented by `*`.
```text
********
********
**N*****
********
********
********
******N*
N*******
```
Here it is again with attacked empty squares marked as `a`. The required output is the number of remaining squares (the number of squares still showing `*`).
```text
*a*a****
a***a***
**N*****
a***a***
*a*a*a*a
*a**a***
**a***N*
N***a***
```
So for this example, the output would be `47`.
## Test cases
### String input test cases
Test case inputs are given as 8 strings of 8 characters, followed by the output as an integer. Knights are represented by `N` and empty squares are represented by `*`.
```text
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
64
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
0
],
[
[
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
],
0
],
[
[
"N***N***",
"*N***N**",
"**N***N*",
"***N***N",
"N***N***",
"*N***N**",
"**N***N*",
"***N***N",
],
16
],
[
[
"N*******",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
61
],
[
[
"******N*",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
60
],
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"********",
"*****N**",
],
59
],
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"*N******",
"********",
],
59
],
[
[
"********",
"**N*****",
"********",
"********",
"********",
"********",
"********",
"********",
],
57
],
[
[
"********",
"********",
"**N*****",
"********",
"********",
"********",
"********",
"********",
],
55
],
[
[
"********",
"********",
"****N***",
"********",
"***N****",
"********",
"********",
"********",
],
48
],
[
[
"********",
"********",
"***N****",
"*****N**",
"**N*****",
"****N***",
"********",
"********",
],
36
],
[
[
"NNNNNNNN",
"NNN*N*NN",
"NN*NNN*N",
"NNNN*NNN",
"NN*NNN*N",
"NNN*N*NN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNNNN",
"NNN*N*NN",
"N***NN*N",
"*NNN*NNN",
"NN*NNN*N",
"*NN***NN",
"N*N*NNNN",
"NNNNNNNN",
],
2
],
[
[
"*NNNNNNN",
"NN*NNNNN",
"N*NNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNN*N",
"NNNN*NNN",
"NNNNN*N*",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNN*N*N",
"NNN*NNN*",
"NNNNN*NN",
],
1
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"*N*NNNNN",
"NNN*NNNN",
"N*NNNNNN",
"NNN*NNNN",
],
1
],
[
[
"*NNN*NNN",
"NN*NNNNN",
"*NNN*NNN",
"N*N*NNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"N*N*NNNN",
"*NNN*NNN",
"NN*NNNNN",
"*NNN*NNN",
"N*N*NNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"********",
"********",
"**N*****",
"********",
"********",
"********",
"******N*",
"N*******",
],
47
]
```
### Integer input test cases
If you choose to take input as a 64 bit unsigned integer, with each square being represented by a single bit, these are the equivalent of the test cases shown above, but with integer input.
Input which treats `1` bits as knights will be called ***one_knight_input***, and input which treats `0` bits as knights will be called ***zero_knight_input***. Since both of these are valid input types, both are included in the test cases so you can choose which to use.
Each test case is in the format `one_knight_input : zero_knight_input : output`.
```text
0 : 18446744073709551615 : 64
18446744073709551615 : 0 : 0
12273903644374837845 : 6172840429334713770 : 0
9819010546270478865 : 8627733527439072750 : 16
9223372036854775808 : 9223372036854775807 : 61
144115188075855872 : 18302628885633695743 : 60
4 : 18446744073709551611 : 59
16384 : 18446744073709535231 : 59
9007199254740992 : 18437736874454810623 : 57
35184372088832 : 18446708889337462783 : 55
8796361457664 : 18446735277348093951 : 48
17609903308800 : 18446726463806242815 : 36
18441077155848519679 : 5666917861031936 : 1
18440988645153550335 : 5755428556001280 : 2
9214294468855857151 : 9232449604853694464 : 1
18300371588261871615 : 146372485447680000 : 1
18446744073708891899 : 659716 : 1
18446744071024132079 : 2685419536 : 1
8637754208117850111 : 9808989865591701504 : 1
12643820184012849151 : 5802923889696702464 : 1
35184372089472 : 18446708889337462143 : 47
```
> Explanations are optional, but I'm more likely to upvote answers that have one.

#8: Post edited by

trichoplax‭ · 2022-10-25T01:56:17Z (about 2 years ago)
Reverse test edit

Copy Link

Raw

Markdown

Given a chess board with some knights on it, say how many squares are neither attacked by a knight nor containing a knight.
# Input
- An 8 by 8 grid where each square is either a knight or empty
- The input can contain any number of knights from 0 to 64
- You may choose to take input with any 2 distinct characters (or numbers or Booleans - there is no restriction to string input) representing a knight and an empty square
- You may take input in the format of your choice provided it does not provide additional information that would help solve the challenge
- For example, if you find it more convenient you could take input as a single 64 bit integer, where each bit is 1 for a knight and 0 for an empty square
# Output
- A number from 0 to 64, indicating the number of squares that satisfy both of:
- The square does not contain a knight
- The square is not a knight's move away from a knight.
A knight's move is either of:
- 2 squares horizontally (left or right) and 1 square vertically (up or down)
- 1 square horizontally (left or right) and 2 squares vertically (up or down)
[![Knight's moves shown as dots](https://codegolf.codidact.com/uploads/Q4kXyQDf3HZiX5NWncgRS2Fi)](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "View on Wikipedia")
(thanks to [Wikipedia](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "Wikipedia section on Knight's moves"))
# Example
The following example input has knights represented by `N` and empty squares represented by `*`.
```text
********
********
**N*****
********
********
********
******N*
N*******
```
Here it is again with attacked empty squares marked as `a`. The required output is the number of remaining squares (the number of squares still showing `*`).
```text
*a*a****
a***a***
**N*****
a***a***
*a*a*a*a
*a**a***
**a***N*
N***a***
```
So for this example, the output would be `47`.
# Test cases
~~## Test cases~~
### String input test cases
Test case inputs are given as 8 strings of 8 characters, followed by the output as an integer. Knights are represented by `N` and empty squares are represented by `*`.
```text
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
64
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
0
],
[
[
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
],
0
],
[
[
"N***N***",
"*N***N**",
"**N***N*",
"***N***N",
"N***N***",
"*N***N**",
"**N***N*",
"***N***N",
],
16
],
[
[
"N*******",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
61
],
[
[
"******N*",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
60
],
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"********",
"*****N**",
],
59
],
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"*N******",
"********",
],
59
],
[
[
"********",
"**N*****",
"********",
"********",
"********",
"********",
"********",
"********",
],
57
],
[
[
"********",
"********",
"**N*****",
"********",
"********",
"********",
"********",
"********",
],
55
],
[
[
"********",
"********",
"****N***",
"********",
"***N****",
"********",
"********",
"********",
],
48
],
[
[
"********",
"********",
"***N****",
"*****N**",
"**N*****",
"****N***",
"********",
"********",
],
36
],
[
[
"NNNNNNNN",
"NNN*N*NN",
"NN*NNN*N",
"NNNN*NNN",
"NN*NNN*N",
"NNN*N*NN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNNNN",
"NNN*N*NN",
"N***NN*N",
"*NNN*NNN",
"NN*NNN*N",
"*NN***NN",
"N*N*NNNN",
"NNNNNNNN",
],
2
],
[
[
"*NNNNNNN",
"NN*NNNNN",
"N*NNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNN*N",
"NNNN*NNN",
"NNNNN*N*",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNN*N*N",
"NNN*NNN*",
"NNNNN*NN",
],
1
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"*N*NNNNN",
"NNN*NNNN",
"N*NNNNNN",
"NNN*NNNN",
],
1
],
[
[
"*NNN*NNN",
"NN*NNNNN",
"*NNN*NNN",
"N*N*NNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"N*N*NNNN",
"*NNN*NNN",
"NN*NNNNN",
"*NNN*NNN",
"N*N*NNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"********",
"********",
"**N*****",
"********",
"********",
"********",
"******N*",
"N*******",
],
47
]
```
### Integer input test cases
If you choose to take input as a 64 bit unsigned integer, with each square being represented by a single bit, these are the equivalent of the test cases shown above, but with integer input.
Input which treats `1` bits as knights will be called ***one_knight_input***, and input which treats `0` bits as knights will be called ***zero_knight_input***. Since both of these are valid input types, both are included in the test cases so you can choose which to use.
Each test case is in the format `one_knight_input : zero_knight_input : output`.
```text
0 : 18446744073709551615 : 64
18446744073709551615 : 0 : 0
12273903644374837845 : 6172840429334713770 : 0
9819010546270478865 : 8627733527439072750 : 16
9223372036854775808 : 9223372036854775807 : 61
144115188075855872 : 18302628885633695743 : 60
4 : 18446744073709551611 : 59
16384 : 18446744073709535231 : 59
9007199254740992 : 18437736874454810623 : 57
35184372088832 : 18446708889337462783 : 55
8796361457664 : 18446735277348093951 : 48
17609903308800 : 18446726463806242815 : 36
18441077155848519679 : 5666917861031936 : 1
18440988645153550335 : 5755428556001280 : 2
9214294468855857151 : 9232449604853694464 : 1
18300371588261871615 : 146372485447680000 : 1
18446744073708891899 : 659716 : 1
18446744071024132079 : 2685419536 : 1
8637754208117850111 : 9808989865591701504 : 1
12643820184012849151 : 5802923889696702464 : 1
35184372089472 : 18446708889337462143 : 47
```
> Explanations are optional, but I'm more likely to upvote answers that have one.

Given a chess board with some knights on it, say how many squares are neither attacked by a knight nor containing a knight.
# Input
- An 8 by 8 grid where each square is either a knight or empty
- The input can contain any number of knights from 0 to 64
- You may choose to take input with any 2 distinct characters (or numbers or Booleans - there is no restriction to string input) representing a knight and an empty square
- You may take input in the format of your choice provided it does not provide additional information that would help solve the challenge
- For example, if you find it more convenient you could take input as a single 64 bit integer, where each bit is 1 for a knight and 0 for an empty square
# Output
- A number from 0 to 64, indicating the number of squares that satisfy both of:
- The square does not contain a knight
- The square is not a knight's move away from a knight.
A knight's move is either of:
- 2 squares horizontally (left or right) and 1 square vertically (up or down)
- 1 square horizontally (left or right) and 2 squares vertically (up or down)
[![Knight's moves shown as dots](https://codegolf.codidact.com/uploads/Q4kXyQDf3HZiX5NWncgRS2Fi)](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "View on Wikipedia")
(thanks to [Wikipedia](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "Wikipedia section on Knight's moves"))
# Example
The following example input has knights represented by `N` and empty squares represented by `*`.
```text
********
********
**N*****
********
********
********
******N*
N*******
```
Here it is again with attacked empty squares marked as `a`. The required output is the number of remaining squares (the number of squares still showing `*`).
```text
*a*a****
a***a***
**N*****
a***a***
*a*a*a*a
*a**a***
**a***N*
N***a***
```
So for this example, the output would be `47`.
# Test cases
### String input test cases
Test case inputs are given as 8 strings of 8 characters, followed by the output as an integer. Knights are represented by `N` and empty squares are represented by `*`.
```text
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
64
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
0
],
[
[
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
],
0
],
[
[
"N***N***",
"*N***N**",
"**N***N*",
"***N***N",
"N***N***",
"*N***N**",
"**N***N*",
"***N***N",
],
16
],
[
[
"N*******",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
61
],
[
[
"******N*",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
60
],
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"********",
"*****N**",
],
59
],
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"*N******",
"********",
],
59
],
[
[
"********",
"**N*****",
"********",
"********",
"********",
"********",
"********",
"********",
],
57
],
[
[
"********",
"********",
"**N*****",
"********",
"********",
"********",
"********",
"********",
],
55
],
[
[
"********",
"********",
"****N***",
"********",
"***N****",
"********",
"********",
"********",
],
48
],
[
[
"********",
"********",
"***N****",
"*****N**",
"**N*****",
"****N***",
"********",
"********",
],
36
],
[
[
"NNNNNNNN",
"NNN*N*NN",
"NN*NNN*N",
"NNNN*NNN",
"NN*NNN*N",
"NNN*N*NN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNNNN",
"NNN*N*NN",
"N***NN*N",
"*NNN*NNN",
"NN*NNN*N",
"*NN***NN",
"N*N*NNNN",
"NNNNNNNN",
],
2
],
[
[
"*NNNNNNN",
"NN*NNNNN",
"N*NNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNN*N",
"NNNN*NNN",
"NNNNN*N*",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNN*N*N",
"NNN*NNN*",
"NNNNN*NN",
],
1
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"*N*NNNNN",
"NNN*NNNN",
"N*NNNNNN",
"NNN*NNNN",
],
1
],
[
[
"*NNN*NNN",
"NN*NNNNN",
"*NNN*NNN",
"N*N*NNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"N*N*NNNN",
"*NNN*NNN",
"NN*NNNNN",
"*NNN*NNN",
"N*N*NNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"********",
"********",
"**N*****",
"********",
"********",
"********",
"******N*",
"N*******",
],
47
]
```
### Integer input test cases
If you choose to take input as a 64 bit unsigned integer, with each square being represented by a single bit, these are the equivalent of the test cases shown above, but with integer input.
Input which treats `1` bits as knights will be called ***one_knight_input***, and input which treats `0` bits as knights will be called ***zero_knight_input***. Since both of these are valid input types, both are included in the test cases so you can choose which to use.
Each test case is in the format `one_knight_input : zero_knight_input : output`.
```text
0 : 18446744073709551615 : 64
18446744073709551615 : 0 : 0
12273903644374837845 : 6172840429334713770 : 0
9819010546270478865 : 8627733527439072750 : 16
9223372036854775808 : 9223372036854775807 : 61
144115188075855872 : 18302628885633695743 : 60
4 : 18446744073709551611 : 59
16384 : 18446744073709535231 : 59
9007199254740992 : 18437736874454810623 : 57
35184372088832 : 18446708889337462783 : 55
8796361457664 : 18446735277348093951 : 48
17609903308800 : 18446726463806242815 : 36
18441077155848519679 : 5666917861031936 : 1
18440988645153550335 : 5755428556001280 : 2
9214294468855857151 : 9232449604853694464 : 1
18300371588261871615 : 146372485447680000 : 1
18446744073708891899 : 659716 : 1
18446744071024132079 : 2685419536 : 1
8637754208117850111 : 9808989865591701504 : 1
12643820184012849151 : 5802923889696702464 : 1
35184372089472 : 18446708889337462143 : 47
```
> Explanations are optional, but I'm more likely to upvote answers that have one.

#7: Post edited by

trichoplax‭ · 2022-10-25T01:55:26Z (about 2 years ago)
Test edit

Copy Link

Raw

Markdown

Given a chess board with some knights on it, say how many squares are neither attacked by a knight nor containing a knight.
# Input
- An 8 by 8 grid where each square is either a knight or empty
- The input can contain any number of knights from 0 to 64
- You may choose to take input with any 2 distinct characters (or numbers or Booleans - there is no restriction to string input) representing a knight and an empty square
- You may take input in the format of your choice provided it does not provide additional information that would help solve the challenge
- For example, if you find it more convenient you could take input as a single 64 bit integer, where each bit is 1 for a knight and 0 for an empty square
# Output
- A number from 0 to 64, indicating the number of squares that satisfy both of:
- The square does not contain a knight
- The square is not a knight's move away from a knight.
A knight's move is either of:
- 2 squares horizontally (left or right) and 1 square vertically (up or down)
- 1 square horizontally (left or right) and 2 squares vertically (up or down)
[![Knight's moves shown as dots](https://codegolf.codidact.com/uploads/Q4kXyQDf3HZiX5NWncgRS2Fi)](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "View on Wikipedia")
(thanks to [Wikipedia](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "Wikipedia section on Knight's moves"))
# Example
The following example input has knights represented by `N` and empty squares represented by `*`.
```text
********
********
**N*****
********
********
********
******N*
N*******
```
Here it is again with attacked empty squares marked as `a`. The required output is the number of remaining squares (the number of squares still showing `*`).
```text
*a*a****
a***a***
**N*****
a***a***
*a*a*a*a
*a**a***
**a***N*
N***a***
```
So for this example, the output would be `47`.
# Test cases
### String input test cases
Test case inputs are given as 8 strings of 8 characters, followed by the output as an integer. Knights are represented by `N` and empty squares are represented by `*`.
```text
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
64
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
0
],
[
[
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
],
0
],
[
[
"N***N***",
"*N***N**",
"**N***N*",
"***N***N",
"N***N***",
"*N***N**",
"**N***N*",
"***N***N",
],
16
],
[
[
"N*******",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
61
],
[
[
"******N*",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
60
],
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"********",
"*****N**",
],
59
],
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"*N******",
"********",
],
59
],
[
[
"********",
"**N*****",
"********",
"********",
"********",
"********",
"********",
"********",
],
57
],
[
[
"********",
"********",
"**N*****",
"********",
"********",
"********",
"********",
"********",
],
55
],
[
[
"********",
"********",
"****N***",
"********",
"***N****",
"********",
"********",
"********",
],
48
],
[
[
"********",
"********",
"***N****",
"*****N**",
"**N*****",
"****N***",
"********",
"********",
],
36
],
[
[
"NNNNNNNN",
"NNN*N*NN",
"NN*NNN*N",
"NNNN*NNN",
"NN*NNN*N",
"NNN*N*NN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNNNN",
"NNN*N*NN",
"N***NN*N",
"*NNN*NNN",
"NN*NNN*N",
"*NN***NN",
"N*N*NNNN",
"NNNNNNNN",
],
2
],
[
[
"*NNNNNNN",
"NN*NNNNN",
"N*NNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNN*N",
"NNNN*NNN",
"NNNNN*N*",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNN*N*N",
"NNN*NNN*",
"NNNNN*NN",
],
1
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"*N*NNNNN",
"NNN*NNNN",
"N*NNNNNN",
"NNN*NNNN",
],
1
],
[
[
"*NNN*NNN",
"NN*NNNNN",
"*NNN*NNN",
"N*N*NNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"N*N*NNNN",
"*NNN*NNN",
"NN*NNNNN",
"*NNN*NNN",
"N*N*NNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"********",
"********",
"**N*****",
"********",
"********",
"********",
"******N*",
"N*******",
],
47
]
```
### Integer input test cases
If you choose to take input as a 64 bit unsigned integer, with each square being represented by a single bit, these are the equivalent of the test cases shown above, but with integer input.
Input which treats `1` bits as knights will be called ***one_knight_input***, and input which treats `0` bits as knights will be called ***zero_knight_input***. Since both of these are valid input types, both are included in the test cases so you can choose which to use.
Each test case is in the format `one_knight_input : zero_knight_input : output`.
```text
0 : 18446744073709551615 : 64
18446744073709551615 : 0 : 0
12273903644374837845 : 6172840429334713770 : 0
9819010546270478865 : 8627733527439072750 : 16
9223372036854775808 : 9223372036854775807 : 61
144115188075855872 : 18302628885633695743 : 60
4 : 18446744073709551611 : 59
16384 : 18446744073709535231 : 59
9007199254740992 : 18437736874454810623 : 57
35184372088832 : 18446708889337462783 : 55
8796361457664 : 18446735277348093951 : 48
17609903308800 : 18446726463806242815 : 36
18441077155848519679 : 5666917861031936 : 1
18440988645153550335 : 5755428556001280 : 2
9214294468855857151 : 9232449604853694464 : 1
18300371588261871615 : 146372485447680000 : 1
18446744073708891899 : 659716 : 1
18446744071024132079 : 2685419536 : 1
8637754208117850111 : 9808989865591701504 : 1
12643820184012849151 : 5802923889696702464 : 1
35184372089472 : 18446708889337462143 : 47
```
> Explanations are optional, but I'm more likely to upvote answers that have one.

Given a chess board with some knights on it, say how many squares are neither attacked by a knight nor containing a knight.
# Input
- An 8 by 8 grid where each square is either a knight or empty
- The input can contain any number of knights from 0 to 64
- You may choose to take input with any 2 distinct characters (or numbers or Booleans - there is no restriction to string input) representing a knight and an empty square
- You may take input in the format of your choice provided it does not provide additional information that would help solve the challenge
- For example, if you find it more convenient you could take input as a single 64 bit integer, where each bit is 1 for a knight and 0 for an empty square
# Output
- A number from 0 to 64, indicating the number of squares that satisfy both of:
- The square does not contain a knight
- The square is not a knight's move away from a knight.
A knight's move is either of:
- 2 squares horizontally (left or right) and 1 square vertically (up or down)
- 1 square horizontally (left or right) and 2 squares vertically (up or down)
[![Knight's moves shown as dots](https://codegolf.codidact.com/uploads/Q4kXyQDf3HZiX5NWncgRS2Fi)](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "View on Wikipedia")
(thanks to [Wikipedia](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "Wikipedia section on Knight's moves"))
# Example
The following example input has knights represented by `N` and empty squares represented by `*`.
```text
********
********
**N*****
********
********
********
******N*
N*******
```
Here it is again with attacked empty squares marked as `a`. The required output is the number of remaining squares (the number of squares still showing `*`).
```text
*a*a****
a***a***
**N*****
a***a***
*a*a*a*a
*a**a***
**a***N*
N***a***
```
So for this example, the output would be `47`.
# Test cases
## Test cases
### String input test cases
Test case inputs are given as 8 strings of 8 characters, followed by the output as an integer. Knights are represented by `N` and empty squares are represented by `*`.
```text
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
64
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
0
],
[
[
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
],
0
],
[
[
"N***N***",
"*N***N**",
"**N***N*",
"***N***N",
"N***N***",
"*N***N**",
"**N***N*",
"***N***N",
],
16
],
[
[
"N*******",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
61
],
[
[
"******N*",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
60
],
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"********",
"*****N**",
],
59
],
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"*N******",
"********",
],
59
],
[
[
"********",
"**N*****",
"********",
"********",
"********",
"********",
"********",
"********",
],
57
],
[
[
"********",
"********",
"**N*****",
"********",
"********",
"********",
"********",
"********",
],
55
],
[
[
"********",
"********",
"****N***",
"********",
"***N****",
"********",
"********",
"********",
],
48
],
[
[
"********",
"********",
"***N****",
"*****N**",
"**N*****",
"****N***",
"********",
"********",
],
36
],
[
[
"NNNNNNNN",
"NNN*N*NN",
"NN*NNN*N",
"NNNN*NNN",
"NN*NNN*N",
"NNN*N*NN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNNNN",
"NNN*N*NN",
"N***NN*N",
"*NNN*NNN",
"NN*NNN*N",
"*NN***NN",
"N*N*NNNN",
"NNNNNNNN",
],
2
],
[
[
"*NNNNNNN",
"NN*NNNNN",
"N*NNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNN*N",
"NNNN*NNN",
"NNNNN*N*",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNN*N*N",
"NNN*NNN*",
"NNNNN*NN",
],
1
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"*N*NNNNN",
"NNN*NNNN",
"N*NNNNNN",
"NNN*NNNN",
],
1
],
[
[
"*NNN*NNN",
"NN*NNNNN",
"*NNN*NNN",
"N*N*NNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"N*N*NNNN",
"*NNN*NNN",
"NN*NNNNN",
"*NNN*NNN",
"N*N*NNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"********",
"********",
"**N*****",
"********",
"********",
"********",
"******N*",
"N*******",
],
47
]
```
### Integer input test cases
If you choose to take input as a 64 bit unsigned integer, with each square being represented by a single bit, these are the equivalent of the test cases shown above, but with integer input.
Input which treats `1` bits as knights will be called ***one_knight_input***, and input which treats `0` bits as knights will be called ***zero_knight_input***. Since both of these are valid input types, both are included in the test cases so you can choose which to use.
Each test case is in the format `one_knight_input : zero_knight_input : output`.
```text
0 : 18446744073709551615 : 64
18446744073709551615 : 0 : 0
12273903644374837845 : 6172840429334713770 : 0
9819010546270478865 : 8627733527439072750 : 16
9223372036854775808 : 9223372036854775807 : 61
144115188075855872 : 18302628885633695743 : 60
4 : 18446744073709551611 : 59
16384 : 18446744073709535231 : 59
9007199254740992 : 18437736874454810623 : 57
35184372088832 : 18446708889337462783 : 55
8796361457664 : 18446735277348093951 : 48
17609903308800 : 18446726463806242815 : 36
18441077155848519679 : 5666917861031936 : 1
18440988645153550335 : 5755428556001280 : 2
9214294468855857151 : 9232449604853694464 : 1
18300371588261871615 : 146372485447680000 : 1
18446744073708891899 : 659716 : 1
18446744071024132079 : 2685419536 : 1
8637754208117850111 : 9808989865591701504 : 1
12643820184012849151 : 5802923889696702464 : 1
35184372089472 : 18446708889337462143 : 47
```
> Explanations are optional, but I'm more likely to upvote answers that have one.

#6: Post edited by

trichoplax‭ · 2022-10-25T01:30:59Z (about 2 years ago)
Demote heading2 to heading3 as heading1 is automatically demoted

Copy Link

Raw

Markdown

Given a chess board with some knights on it, say how many squares are neither attacked by a knight nor containing a knight.
# Input
- An 8 by 8 grid where each square is either a knight or empty
- The input can contain any number of knights from 0 to 64
- You may choose to take input with any 2 distinct characters (or numbers or Booleans - there is no restriction to string input) representing a knight and an empty square
- You may take input in the format of your choice provided it does not provide additional information that would help solve the challenge
- For example, if you find it more convenient you could take input as a single 64 bit integer, where each bit is 1 for a knight and 0 for an empty square
# Output
- A number from 0 to 64, indicating the number of squares that satisfy both of:
- The square does not contain a knight
- The square is not a knight's move away from a knight.
A knight's move is either of:
- 2 squares horizontally (left or right) and 1 square vertically (up or down)
- 1 square horizontally (left or right) and 2 squares vertically (up or down)
[![Knight's moves shown as dots](https://codegolf.codidact.com/uploads/Q4kXyQDf3HZiX5NWncgRS2Fi)](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "View on Wikipedia")
(thanks to [Wikipedia](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "Wikipedia section on Knight's moves"))
# Example
The following example input has knights represented by `N` and empty squares represented by `*`.
```text
********
********
**N*****
********
********
********
******N*
N*******
```
Here it is again with attacked empty squares marked as `a`. The required output is the number of remaining squares (the number of squares still showing `*`).
```text
*a*a****
a***a***
**N*****
a***a***
*a*a*a*a
*a**a***
**a***N*
N***a***
```
So for this example, the output would be `47`.
# Test cases
~~## String input test cases~~
Test case inputs are given as 8 strings of 8 characters, followed by the output as an integer. Knights are represented by `N` and empty squares are represented by `*`.
```text
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
64
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
0
],
[
[
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
],
0
],
[
[
"N***N***",
"*N***N**",
"**N***N*",
"***N***N",
"N***N***",
"*N***N**",
"**N***N*",
"***N***N",
],
16
],
[
[
"N*******",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
61
],
[
[
"******N*",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
60
],
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"********",
"*****N**",
],
59
],
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"*N******",
"********",
],
59
],
[
[
"********",
"**N*****",
"********",
"********",
"********",
"********",
"********",
"********",
],
57
],
[
[
"********",
"********",
"**N*****",
"********",
"********",
"********",
"********",
"********",
],
55
],
[
[
"********",
"********",
"****N***",
"********",
"***N****",
"********",
"********",
"********",
],
48
],
[
[
"********",
"********",
"***N****",
"*****N**",
"**N*****",
"****N***",
"********",
"********",
],
36
],
[
[
"NNNNNNNN",
"NNN*N*NN",
"NN*NNN*N",
"NNNN*NNN",
"NN*NNN*N",
"NNN*N*NN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNNNN",
"NNN*N*NN",
"N***NN*N",
"*NNN*NNN",
"NN*NNN*N",
"*NN***NN",
"N*N*NNNN",
"NNNNNNNN",
],
2
],
[
[
"*NNNNNNN",
"NN*NNNNN",
"N*NNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNN*N",
"NNNN*NNN",
"NNNNN*N*",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNN*N*N",
"NNN*NNN*",
"NNNNN*NN",
],
1
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"*N*NNNNN",
"NNN*NNNN",
"N*NNNNNN",
"NNN*NNNN",
],
1
],
[
[
"*NNN*NNN",
"NN*NNNNN",
"*NNN*NNN",
"N*N*NNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"N*N*NNNN",
"*NNN*NNN",
"NN*NNNNN",
"*NNN*NNN",
"N*N*NNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"********",
"********",
"**N*****",
"********",
"********",
"********",
"******N*",
"N*******",
],
47
]
```
~~## Integer input test cases~~
If you choose to take input as a 64 bit unsigned integer, with each square being represented by a single bit, these are the equivalent of the test cases shown above, but with integer input.
Input which treats `1` bits as knights will be called ***one_knight_input***, and input which treats `0` bits as knights will be called ***zero_knight_input***. Since both of these are valid input types, both are included in the test cases so you can choose which to use.
Each test case is in the format `one_knight_input : zero_knight_input : output`.
```text
0 : 18446744073709551615 : 64
18446744073709551615 : 0 : 0
12273903644374837845 : 6172840429334713770 : 0
9819010546270478865 : 8627733527439072750 : 16
9223372036854775808 : 9223372036854775807 : 61
144115188075855872 : 18302628885633695743 : 60
4 : 18446744073709551611 : 59
16384 : 18446744073709535231 : 59
9007199254740992 : 18437736874454810623 : 57
35184372088832 : 18446708889337462783 : 55
8796361457664 : 18446735277348093951 : 48
17609903308800 : 18446726463806242815 : 36
18441077155848519679 : 5666917861031936 : 1
18440988645153550335 : 5755428556001280 : 2
9214294468855857151 : 9232449604853694464 : 1
18300371588261871615 : 146372485447680000 : 1
18446744073708891899 : 659716 : 1
18446744071024132079 : 2685419536 : 1
8637754208117850111 : 9808989865591701504 : 1
12643820184012849151 : 5802923889696702464 : 1
35184372089472 : 18446708889337462143 : 47
```
> Explanations are optional, but I'm more likely to upvote answers that have one.

Given a chess board with some knights on it, say how many squares are neither attacked by a knight nor containing a knight.
# Input
- An 8 by 8 grid where each square is either a knight or empty
- The input can contain any number of knights from 0 to 64
- You may choose to take input with any 2 distinct characters (or numbers or Booleans - there is no restriction to string input) representing a knight and an empty square
- You may take input in the format of your choice provided it does not provide additional information that would help solve the challenge
- For example, if you find it more convenient you could take input as a single 64 bit integer, where each bit is 1 for a knight and 0 for an empty square
# Output
- A number from 0 to 64, indicating the number of squares that satisfy both of:
- The square does not contain a knight
- The square is not a knight's move away from a knight.
A knight's move is either of:
- 2 squares horizontally (left or right) and 1 square vertically (up or down)
- 1 square horizontally (left or right) and 2 squares vertically (up or down)
[![Knight's moves shown as dots](https://codegolf.codidact.com/uploads/Q4kXyQDf3HZiX5NWncgRS2Fi)](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "View on Wikipedia")
(thanks to [Wikipedia](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "Wikipedia section on Knight's moves"))
# Example
The following example input has knights represented by `N` and empty squares represented by `*`.
```text
********
********
**N*****
********
********
********
******N*
N*******
```
Here it is again with attacked empty squares marked as `a`. The required output is the number of remaining squares (the number of squares still showing `*`).
```text
*a*a****
a***a***
**N*****
a***a***
*a*a*a*a
*a**a***
**a***N*
N***a***
```
So for this example, the output would be `47`.
# Test cases
### String input test cases
Test case inputs are given as 8 strings of 8 characters, followed by the output as an integer. Knights are represented by `N` and empty squares are represented by `*`.
```text
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
64
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
0
],
[
[
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
],
0
],
[
[
"N***N***",
"*N***N**",
"**N***N*",
"***N***N",
"N***N***",
"*N***N**",
"**N***N*",
"***N***N",
],
16
],
[
[
"N*******",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
61
],
[
[
"******N*",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
60
],
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"********",
"*****N**",
],
59
],
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"*N******",
"********",
],
59
],
[
[
"********",
"**N*****",
"********",
"********",
"********",
"********",
"********",
"********",
],
57
],
[
[
"********",
"********",
"**N*****",
"********",
"********",
"********",
"********",
"********",
],
55
],
[
[
"********",
"********",
"****N***",
"********",
"***N****",
"********",
"********",
"********",
],
48
],
[
[
"********",
"********",
"***N****",
"*****N**",
"**N*****",
"****N***",
"********",
"********",
],
36
],
[
[
"NNNNNNNN",
"NNN*N*NN",
"NN*NNN*N",
"NNNN*NNN",
"NN*NNN*N",
"NNN*N*NN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNNNN",
"NNN*N*NN",
"N***NN*N",
"*NNN*NNN",
"NN*NNN*N",
"*NN***NN",
"N*N*NNNN",
"NNNNNNNN",
],
2
],
[
[
"*NNNNNNN",
"NN*NNNNN",
"N*NNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNN*N",
"NNNN*NNN",
"NNNNN*N*",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNN*N*N",
"NNN*NNN*",
"NNNNN*NN",
],
1
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"*N*NNNNN",
"NNN*NNNN",
"N*NNNNNN",
"NNN*NNNN",
],
1
],
[
[
"*NNN*NNN",
"NN*NNNNN",
"*NNN*NNN",
"N*N*NNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"N*N*NNNN",
"*NNN*NNN",
"NN*NNNNN",
"*NNN*NNN",
"N*N*NNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"********",
"********",
"**N*****",
"********",
"********",
"********",
"******N*",
"N*******",
],
47
]
```
### Integer input test cases
If you choose to take input as a 64 bit unsigned integer, with each square being represented by a single bit, these are the equivalent of the test cases shown above, but with integer input.
Input which treats `1` bits as knights will be called ***one_knight_input***, and input which treats `0` bits as knights will be called ***zero_knight_input***. Since both of these are valid input types, both are included in the test cases so you can choose which to use.
Each test case is in the format `one_knight_input : zero_knight_input : output`.
```text
0 : 18446744073709551615 : 64
18446744073709551615 : 0 : 0
12273903644374837845 : 6172840429334713770 : 0
9819010546270478865 : 8627733527439072750 : 16
9223372036854775808 : 9223372036854775807 : 61
144115188075855872 : 18302628885633695743 : 60
4 : 18446744073709551611 : 59
16384 : 18446744073709535231 : 59
9007199254740992 : 18437736874454810623 : 57
35184372088832 : 18446708889337462783 : 55
8796361457664 : 18446735277348093951 : 48
17609903308800 : 18446726463806242815 : 36
18441077155848519679 : 5666917861031936 : 1
18440988645153550335 : 5755428556001280 : 2
9214294468855857151 : 9232449604853694464 : 1
18300371588261871615 : 146372485447680000 : 1
18446744073708891899 : 659716 : 1
18446744071024132079 : 2685419536 : 1
8637754208117850111 : 9808989865591701504 : 1
12643820184012849151 : 5802923889696702464 : 1
35184372089472 : 18446708889337462143 : 47
```
> Explanations are optional, but I'm more likely to upvote answers that have one.

#5: Post edited by

trichoplax‭ · 2022-10-25T01:29:02Z (about 2 years ago)
Add equivalent test cases for integer inputs

Copy Link

Raw

Markdown

Given a chess board with some knights on it, say how many squares are neither attacked by a knight nor containing a knight.
~~## Input~~
- An 8 by 8 grid where each square is either a knight or empty
- The input can contain any number of knights from 0 to 64
- You may choose to take input with any 2 distinct characters (or numbers or Booleans - there is no restriction to string input) representing a knight and an empty square
- You may take input in the format of your choice provided it does not provide additional information that would help solve the challenge
- For example, if you find it more convenient you could take input as a single 64 bit integer, where each bit is 1 for a knight and 0 for an empty square
~~## Output~~
- A number from 0 to 64, indicating the number of squares that satisfy both of:
- The square does not contain a knight
- The square is not a knight's move away from a knight.
A knight's move is either of:
- 2 squares horizontally (left or right) and 1 square vertically (up or down)
- 1 square horizontally (left or right) and 2 squares vertically (up or down)
[![Knight's moves shown as dots](https://codegolf.codidact.com/uploads/Q4kXyQDf3HZiX5NWncgRS2Fi)](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "View on Wikipedia")
(thanks to [Wikipedia](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "Wikipedia section on Knight's moves"))
~~## Example~~
The following example input has knights represented by `N` and empty squares represented by `*`.
```text
********
********
**N*****
********
********
********
******N*
N*******
```
Here it is again with attacked empty squares marked as `a`. The required output is the number of remaining squares (the number of squares still showing `*`).
```text
*a*a****
a***a***
**N*****
a***a***
*a*a*a*a
*a**a***
**a***N*
N***a***
```
So for this example, the output would be `47`.
~~## Test cases~~
Test case inputs are given as 8 strings of 8 characters, followed by the output as an integer. Knights are represented by `N` and empty squares are represented by `*`.
```text
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
64
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
0
],
[
[
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
],
0
],
[
[
"N***N***",
"*N***N**",
"**N***N*",
"***N***N",
"N***N***",
"*N***N**",
"**N***N*",
"***N***N",
],
16
],
[
[
"N*******",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
61
],
[
[
"******N*",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
60
],
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"********",
"*****N**",
],
59
],
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"*N******",
"********",
],
59
],
[
[
"********",
"**N*****",
"********",
"********",
"********",
"********",
"********",
"********",
],
57
],
[
[
"********",
"********",
"**N*****",
"********",
"********",
"********",
"********",
"********",
],
55
],
[
[
"********",
"********",
"****N***",
"********",
"***N****",
"********",
"********",
"********",
],
48
],
[
[
"********",
"********",
"***N****",
"*****N**",
"**N*****",
"****N***",
"********",
"********",
],
36
],
[
[
"NNNNNNNN",
"NNN*N*NN",
"NN*NNN*N",
"NNNN*NNN",
"NN*NNN*N",
"NNN*N*NN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNNNN",
"NNN*N*NN",
"N***NN*N",
"*NNN*NNN",
"NN*NNN*N",
"*NN***NN",
"N*N*NNNN",
"NNNNNNNN",
],
2
],
[
[
"*NNNNNNN",
"NN*NNNNN",
"N*NNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNN*N",
"NNNN*NNN",
"NNNNN*N*",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNN*N*N",
"NNN*NNN*",
"NNNNN*NN",
],
1
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"*N*NNNNN",
"NNN*NNNN",
"N*NNNNNN",
"NNN*NNNN",
],
1
],
[
[
"*NNN*NNN",
"NN*NNNNN",
"*NNN*NNN",
"N*N*NNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"N*N*NNNN",
"*NNN*NNN",
"NN*NNNNN",
"*NNN*NNN",
"N*N*NNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"********",
"********",
"**N*****",
"********",
"********",
"********",
"******N*",
"N*******",
],
47
]
```
> Explanations are optional, but I'm more likely to upvote answers that have one.

Given a chess board with some knights on it, say how many squares are neither attacked by a knight nor containing a knight.
# Input
- An 8 by 8 grid where each square is either a knight or empty
- The input can contain any number of knights from 0 to 64
- You may choose to take input with any 2 distinct characters (or numbers or Booleans - there is no restriction to string input) representing a knight and an empty square
- You may take input in the format of your choice provided it does not provide additional information that would help solve the challenge
- For example, if you find it more convenient you could take input as a single 64 bit integer, where each bit is 1 for a knight and 0 for an empty square
# Output
- A number from 0 to 64, indicating the number of squares that satisfy both of:
- The square does not contain a knight
- The square is not a knight's move away from a knight.
A knight's move is either of:
- 2 squares horizontally (left or right) and 1 square vertically (up or down)
- 1 square horizontally (left or right) and 2 squares vertically (up or down)
[![Knight's moves shown as dots](https://codegolf.codidact.com/uploads/Q4kXyQDf3HZiX5NWncgRS2Fi)](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "View on Wikipedia")
(thanks to [Wikipedia](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "Wikipedia section on Knight's moves"))
# Example
The following example input has knights represented by `N` and empty squares represented by `*`.
```text
********
********
**N*****
********
********
********
******N*
N*******
```
Here it is again with attacked empty squares marked as `a`. The required output is the number of remaining squares (the number of squares still showing `*`).
```text
*a*a****
a***a***
**N*****
a***a***
*a*a*a*a
*a**a***
**a***N*
N***a***
```
So for this example, the output would be `47`.
# Test cases
## String input test cases
Test case inputs are given as 8 strings of 8 characters, followed by the output as an integer. Knights are represented by `N` and empty squares are represented by `*`.
```text
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
64
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
0
],
[
[
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
],
0
],
[
[
"N***N***",
"*N***N**",
"**N***N*",
"***N***N",
"N***N***",
"*N***N**",
"**N***N*",
"***N***N",
],
16
],
[
[
"N*******",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
61
],
[
[
"******N*",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
60
],
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"********",
"*****N**",
],
59
],
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"*N******",
"********",
],
59
],
[
[
"********",
"**N*****",
"********",
"********",
"********",
"********",
"********",
"********",
],
57
],
[
[
"********",
"********",
"**N*****",
"********",
"********",
"********",
"********",
"********",
],
55
],
[
[
"********",
"********",
"****N***",
"********",
"***N****",
"********",
"********",
"********",
],
48
],
[
[
"********",
"********",
"***N****",
"*****N**",
"**N*****",
"****N***",
"********",
"********",
],
36
],
[
[
"NNNNNNNN",
"NNN*N*NN",
"NN*NNN*N",
"NNNN*NNN",
"NN*NNN*N",
"NNN*N*NN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNNNN",
"NNN*N*NN",
"N***NN*N",
"*NNN*NNN",
"NN*NNN*N",
"*NN***NN",
"N*N*NNNN",
"NNNNNNNN",
],
2
],
[
[
"*NNNNNNN",
"NN*NNNNN",
"N*NNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNN*N",
"NNNN*NNN",
"NNNNN*N*",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNN*N*N",
"NNN*NNN*",
"NNNNN*NN",
],
1
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"*N*NNNNN",
"NNN*NNNN",
"N*NNNNNN",
"NNN*NNNN",
],
1
],
[
[
"*NNN*NNN",
"NN*NNNNN",
"*NNN*NNN",
"N*N*NNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"N*N*NNNN",
"*NNN*NNN",
"NN*NNNNN",
"*NNN*NNN",
"N*N*NNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"********",
"********",
"**N*****",
"********",
"********",
"********",
"******N*",
"N*******",
],
47
]
```
## Integer input test cases
If you choose to take input as a 64 bit unsigned integer, with each square being represented by a single bit, these are the equivalent of the test cases shown above, but with integer input.
Input which treats `1` bits as knights will be called ***one_knight_input***, and input which treats `0` bits as knights will be called ***zero_knight_input***. Since both of these are valid input types, both are included in the test cases so you can choose which to use.
Each test case is in the format `one_knight_input : zero_knight_input : output`.
```text
0 : 18446744073709551615 : 64
18446744073709551615 : 0 : 0
12273903644374837845 : 6172840429334713770 : 0
9819010546270478865 : 8627733527439072750 : 16
9223372036854775808 : 9223372036854775807 : 61
144115188075855872 : 18302628885633695743 : 60
4 : 18446744073709551611 : 59
16384 : 18446744073709535231 : 59
9007199254740992 : 18437736874454810623 : 57
35184372088832 : 18446708889337462783 : 55
8796361457664 : 18446735277348093951 : 48
17609903308800 : 18446726463806242815 : 36
18441077155848519679 : 5666917861031936 : 1
18440988645153550335 : 5755428556001280 : 2
9214294468855857151 : 9232449604853694464 : 1
18300371588261871615 : 146372485447680000 : 1
18446744073708891899 : 659716 : 1
18446744071024132079 : 2685419536 : 1
8637754208117850111 : 9808989865591701504 : 1
12643820184012849151 : 5802923889696702464 : 1
35184372089472 : 18446708889337462143 : 47
```
> Explanations are optional, but I'm more likely to upvote answers that have one.

#4: Post edited by

trichoplax‭ · 2022-10-23T14:30:18Z (about 2 years ago)
Explicitly allow integer input

Copy Link

Raw

Markdown

Given a chess board with some knights on it, say how many squares are neither attacked by a knight nor containing a knight.
## Input
- An 8 by 8 grid where each square is either a knight or empty
- The input can contain any number of knights from 0 to 64
- You may choose to take input with any 2 distinct characters (or numbers or Booleans - there is no restriction to string input) representing a knight and an empty square
- You may take input in the format of your choice provided it does not provide additional information that would help solve the challenge
## Output
- A number from 0 to 64, indicating the number of squares that satisfy both of:
- The square does not contain a knight
- The square is not a knight's move away from a knight.
A knight's move is either of:
- 2 squares horizontally (left or right) and 1 square vertically (up or down)
- 1 square horizontally (left or right) and 2 squares vertically (up or down)
[![Knight's moves shown as dots](https://codegolf.codidact.com/uploads/Q4kXyQDf3HZiX5NWncgRS2Fi)](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "View on Wikipedia")
(thanks to [Wikipedia](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "Wikipedia section on Knight's moves"))
## Example
The following example input has knights represented by `N` and empty squares represented by `*`.
```text
********
********
**N*****
********
********
********
******N*
N*******
```
Here it is again with attacked empty squares marked as `a`. The required output is the number of remaining squares (the number of squares still showing `*`).
```text
*a*a****
a***a***
**N*****
a***a***
*a*a*a*a
*a**a***
**a***N*
N***a***
```
So for this example, the output would be `47`.
## Test cases
Test case inputs are given as 8 strings of 8 characters, followed by the output as an integer. Knights are represented by `N` and empty squares are represented by `*`.
```text
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
64
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
0
],
[
[
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
],
0
],
[
[
"N***N***",
"*N***N**",
"**N***N*",
"***N***N",
"N***N***",
"*N***N**",
"**N***N*",
"***N***N",
],
16
],
[
[
"N*******",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
61
],
[
[
"******N*",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
60
],
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"********",
"*****N**",
],
59
],
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"*N******",
"********",
],
59
],
[
[
"********",
"**N*****",
"********",
"********",
"********",
"********",
"********",
"********",
],
57
],
[
[
"********",
"********",
"**N*****",
"********",
"********",
"********",
"********",
"********",
],
55
],
[
[
"********",
"********",
"****N***",
"********",
"***N****",
"********",
"********",
"********",
],
48
],
[
[
"********",
"********",
"***N****",
"*****N**",
"**N*****",
"****N***",
"********",
"********",
],
36
],
[
[
"NNNNNNNN",
"NNN*N*NN",
"NN*NNN*N",
"NNNN*NNN",
"NN*NNN*N",
"NNN*N*NN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNNNN",
"NNN*N*NN",
"N***NN*N",
"*NNN*NNN",
"NN*NNN*N",
"*NN***NN",
"N*N*NNNN",
"NNNNNNNN",
],
2
],
[
[
"*NNNNNNN",
"NN*NNNNN",
"N*NNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNN*N",
"NNNN*NNN",
"NNNNN*N*",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNN*N*N",
"NNN*NNN*",
"NNNNN*NN",
],
1
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"*N*NNNNN",
"NNN*NNNN",
"N*NNNNNN",
"NNN*NNNN",
],
1
],
[
[
"*NNN*NNN",
"NN*NNNNN",
"*NNN*NNN",
"N*N*NNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"N*N*NNNN",
"*NNN*NNN",
"NN*NNNNN",
"*NNN*NNN",
"N*N*NNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"********",
"********",
"**N*****",
"********",
"********",
"********",
"******N*",
"N*******",
],
47
]
```
~~> Explanations in answers are optional, but I'm more likely to upvote answers that have one.~~

Given a chess board with some knights on it, say how many squares are neither attacked by a knight nor containing a knight.
## Input
- An 8 by 8 grid where each square is either a knight or empty
- The input can contain any number of knights from 0 to 64
- You may choose to take input with any 2 distinct characters (or numbers or Booleans - there is no restriction to string input) representing a knight and an empty square
- You may take input in the format of your choice provided it does not provide additional information that would help solve the challenge
- For example, if you find it more convenient you could take input as a single 64 bit integer, where each bit is 1 for a knight and 0 for an empty square
## Output
- A number from 0 to 64, indicating the number of squares that satisfy both of:
- The square does not contain a knight
- The square is not a knight's move away from a knight.
A knight's move is either of:
- 2 squares horizontally (left or right) and 1 square vertically (up or down)
- 1 square horizontally (left or right) and 2 squares vertically (up or down)
[![Knight's moves shown as dots](https://codegolf.codidact.com/uploads/Q4kXyQDf3HZiX5NWncgRS2Fi)](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "View on Wikipedia")
(thanks to [Wikipedia](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "Wikipedia section on Knight's moves"))
## Example
The following example input has knights represented by `N` and empty squares represented by `*`.
```text
********
********
**N*****
********
********
********
******N*
N*******
```
Here it is again with attacked empty squares marked as `a`. The required output is the number of remaining squares (the number of squares still showing `*`).
```text
*a*a****
a***a***
**N*****
a***a***
*a*a*a*a
*a**a***
**a***N*
N***a***
```
So for this example, the output would be `47`.
## Test cases
Test case inputs are given as 8 strings of 8 characters, followed by the output as an integer. Knights are represented by `N` and empty squares are represented by `*`.
```text
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
64
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
0
],
[
[
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
],
0
],
[
[
"N***N***",
"*N***N**",
"**N***N*",
"***N***N",
"N***N***",
"*N***N**",
"**N***N*",
"***N***N",
],
16
],
[
[
"N*******",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
61
],
[
[
"******N*",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
60
],
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"********",
"*****N**",
],
59
],
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"*N******",
"********",
],
59
],
[
[
"********",
"**N*****",
"********",
"********",
"********",
"********",
"********",
"********",
],
57
],
[
[
"********",
"********",
"**N*****",
"********",
"********",
"********",
"********",
"********",
],
55
],
[
[
"********",
"********",
"****N***",
"********",
"***N****",
"********",
"********",
"********",
],
48
],
[
[
"********",
"********",
"***N****",
"*****N**",
"**N*****",
"****N***",
"********",
"********",
],
36
],
[
[
"NNNNNNNN",
"NNN*N*NN",
"NN*NNN*N",
"NNNN*NNN",
"NN*NNN*N",
"NNN*N*NN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNNNN",
"NNN*N*NN",
"N***NN*N",
"*NNN*NNN",
"NN*NNN*N",
"*NN***NN",
"N*N*NNNN",
"NNNNNNNN",
],
2
],
[
[
"*NNNNNNN",
"NN*NNNNN",
"N*NNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNN*N",
"NNNN*NNN",
"NNNNN*N*",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNN*N*N",
"NNN*NNN*",
"NNNNN*NN",
],
1
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"*N*NNNNN",
"NNN*NNNN",
"N*NNNNNN",
"NNN*NNNN",
],
1
],
[
[
"*NNN*NNN",
"NN*NNNNN",
"*NNN*NNN",
"N*N*NNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"N*N*NNNN",
"*NNN*NNN",
"NN*NNNNN",
"*NNN*NNN",
"N*N*NNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"********",
"********",
"**N*****",
"********",
"********",
"********",
"******N*",
"N*******",
],
47
]
```
> Explanations are optional, but I'm more likely to upvote answers that have one.

#3: Post edited by

trichoplax‭ · 2022-10-01T03:44:55Z (about 2 years ago)
Make zero knights an explicitly possible input rather than just a test case

Copy Link

Raw

Markdown

Given a chess board with some knights on it, say how many squares are neither attacked by a knight nor containing a knight.
## Input
- An 8 by 8 grid where each square is either a knight or empty
- You may choose to take input with any 2 distinct characters (or numbers or Booleans - there is no restriction to string input) representing a knight and an empty square
- You may take input in the format of your choice provided it does not provide additional information that would help solve the challenge
## Output
- A number from 0 to 64, indicating the number of squares that satisfy both of:
- The square does not contain a knight
- The square is not a knight's move away from a knight.
A knight's move is either of:
- 2 squares horizontally (left or right) and 1 square vertically (up or down)
- 1 square horizontally (left or right) and 2 squares vertically (up or down)
[![Knight's moves shown as dots](https://codegolf.codidact.com/uploads/Q4kXyQDf3HZiX5NWncgRS2Fi)](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "View on Wikipedia")
(thanks to [Wikipedia](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "Wikipedia section on Knight's moves"))
## Example
The following example input has knights represented by `N` and empty squares represented by `*`.
```text
********
********
**N*****
********
********
********
******N*
N*******
```
Here it is again with attacked empty squares marked as `a`. The required output is the number of remaining squares (the number of squares still showing `*`).
```text
*a*a****
a***a***
**N*****
a***a***
*a*a*a*a
*a**a***
**a***N*
N***a***
```
So for this example, the output would be `47`.
## Test cases
Test case inputs are given as 8 strings of 8 characters, followed by the output as an integer. Knights are represented by `N` and empty squares are represented by `*`.
```text
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
64
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
0
],
[
[
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
],
0
],
[
[
"N***N***",
"*N***N**",
"**N***N*",
"***N***N",
"N***N***",
"*N***N**",
"**N***N*",
"***N***N",
],
16
],
[
[
"N*******",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
61
],
[
[
"******N*",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
60
],
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"********",
"*****N**",
],
59
],
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"*N******",
"********",
],
59
],
[
[
"********",
"**N*****",
"********",
"********",
"********",
"********",
"********",
"********",
],
57
],
[
[
"********",
"********",
"**N*****",
"********",
"********",
"********",
"********",
"********",
],
55
],
[
[
"********",
"********",
"****N***",
"********",
"***N****",
"********",
"********",
"********",
],
48
],
[
[
"********",
"********",
"***N****",
"*****N**",
"**N*****",
"****N***",
"********",
"********",
],
36
],
[
[
"NNNNNNNN",
"NNN*N*NN",
"NN*NNN*N",
"NNNN*NNN",
"NN*NNN*N",
"NNN*N*NN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNNNN",
"NNN*N*NN",
"N***NN*N",
"*NNN*NNN",
"NN*NNN*N",
"*NN***NN",
"N*N*NNNN",
"NNNNNNNN",
],
2
],
[
[
"*NNNNNNN",
"NN*NNNNN",
"N*NNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNN*N",
"NNNN*NNN",
"NNNNN*N*",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNN*N*N",
"NNN*NNN*",
"NNNNN*NN",
],
1
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"*N*NNNNN",
"NNN*NNNN",
"N*NNNNNN",
"NNN*NNNN",
],
1
],
[
[
"*NNN*NNN",
"NN*NNNNN",
"*NNN*NNN",
"N*N*NNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"N*N*NNNN",
"*NNN*NNN",
"NN*NNNNN",
"*NNN*NNN",
"N*N*NNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"********",
"********",
"**N*****",
"********",
"********",
"********",
"******N*",
"N*******",
],
47
]
```
> Explanations in answers are optional, but I'm more likely to upvote answers that have one.

Given a chess board with some knights on it, say how many squares are neither attacked by a knight nor containing a knight.
## Input
- An 8 by 8 grid where each square is either a knight or empty
- The input can contain any number of knights from 0 to 64
- You may choose to take input with any 2 distinct characters (or numbers or Booleans - there is no restriction to string input) representing a knight and an empty square
- You may take input in the format of your choice provided it does not provide additional information that would help solve the challenge
## Output
- A number from 0 to 64, indicating the number of squares that satisfy both of:
- The square does not contain a knight
- The square is not a knight's move away from a knight.
A knight's move is either of:
- 2 squares horizontally (left or right) and 1 square vertically (up or down)
- 1 square horizontally (left or right) and 2 squares vertically (up or down)
[![Knight's moves shown as dots](https://codegolf.codidact.com/uploads/Q4kXyQDf3HZiX5NWncgRS2Fi)](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "View on Wikipedia")
(thanks to [Wikipedia](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "Wikipedia section on Knight's moves"))
## Example
The following example input has knights represented by `N` and empty squares represented by `*`.
```text
********
********
**N*****
********
********
********
******N*
N*******
```
Here it is again with attacked empty squares marked as `a`. The required output is the number of remaining squares (the number of squares still showing `*`).
```text
*a*a****
a***a***
**N*****
a***a***
*a*a*a*a
*a**a***
**a***N*
N***a***
```
So for this example, the output would be `47`.
## Test cases
Test case inputs are given as 8 strings of 8 characters, followed by the output as an integer. Knights are represented by `N` and empty squares are represented by `*`.
```text
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
64
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
0
],
[
[
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
],
0
],
[
[
"N***N***",
"*N***N**",
"**N***N*",
"***N***N",
"N***N***",
"*N***N**",
"**N***N*",
"***N***N",
],
16
],
[
[
"N*******",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
61
],
[
[
"******N*",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
60
],
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"********",
"*****N**",
],
59
],
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"*N******",
"********",
],
59
],
[
[
"********",
"**N*****",
"********",
"********",
"********",
"********",
"********",
"********",
],
57
],
[
[
"********",
"********",
"**N*****",
"********",
"********",
"********",
"********",
"********",
],
55
],
[
[
"********",
"********",
"****N***",
"********",
"***N****",
"********",
"********",
"********",
],
48
],
[
[
"********",
"********",
"***N****",
"*****N**",
"**N*****",
"****N***",
"********",
"********",
],
36
],
[
[
"NNNNNNNN",
"NNN*N*NN",
"NN*NNN*N",
"NNNN*NNN",
"NN*NNN*N",
"NNN*N*NN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNNNN",
"NNN*N*NN",
"N***NN*N",
"*NNN*NNN",
"NN*NNN*N",
"*NN***NN",
"N*N*NNNN",
"NNNNNNNN",
],
2
],
[
[
"*NNNNNNN",
"NN*NNNNN",
"N*NNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNN*N",
"NNNN*NNN",
"NNNNN*N*",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNN*N*N",
"NNN*NNN*",
"NNNNN*NN",
],
1
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"*N*NNNNN",
"NNN*NNNN",
"N*NNNNNN",
"NNN*NNNN",
],
1
],
[
[
"*NNN*NNN",
"NN*NNNNN",
"*NNN*NNN",
"N*N*NNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"N*N*NNNN",
"*NNN*NNN",
"NN*NNNNN",
"*NNN*NNN",
"N*N*NNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"********",
"********",
"**N*****",
"********",
"********",
"********",
"******N*",
"N*******",
],
47
]
```
> Explanations in answers are optional, but I'm more likely to upvote answers that have one.

#2: Post edited by

trichoplax‭ · 2022-09-30T22:52:58Z (about 2 years ago)
Explicitly rule in Boolean input

Copy Link

Raw

Markdown

Given a chess board with some knights on it, say how many squares are neither attacked by a knight nor containing a knight.
## Input
- An 8 by 8 grid where each square is either a knight or empty
~~- You may choose to take input with any 2 distinct characters representing a knight and an empty square~~
- You may take input in the format of your choice provided it does not provide additional information that would help solve the challenge
## Output
- A number from 0 to 64, indicating the number of squares that satisfy both of:
- The square does not contain a knight
- The square is not a knight's move away from a knight.
A knight's move is either of:
- 2 squares horizontally (left or right) and 1 square vertically (up or down)
- 1 square horizontally (left or right) and 2 squares vertically (up or down)
[![Knight's moves shown as dots](https://codegolf.codidact.com/uploads/Q4kXyQDf3HZiX5NWncgRS2Fi)](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "View on Wikipedia")
(thanks to [Wikipedia](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "Wikipedia section on Knight's moves"))
## Example
The following example input has knights represented by `N` and empty squares represented by `*`.
```text
********
********
**N*****
********
********
********
******N*
N*******
```
Here it is again with attacked empty squares marked as `a`. The required output is the number of remaining squares (the number of squares still showing `*`).
```text
*a*a****
a***a***
**N*****
a***a***
*a*a*a*a
*a**a***
**a***N*
N***a***
```
So for this example, the output would be `47`.
## Test cases
Test case inputs are given as 8 strings of 8 characters, followed by the output as an integer. Knights are represented by `N` and empty squares are represented by `*`.
```text
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
64
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
0
],
[
[
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
],
0
],
[
[
"N***N***",
"*N***N**",
"**N***N*",
"***N***N",
"N***N***",
"*N***N**",
"**N***N*",
"***N***N",
],
16
],
[
[
"N*******",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
61
],
[
[
"******N*",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
60
],
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"********",
"*****N**",
],
59
],
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"*N******",
"********",
],
59
],
[
[
"********",
"**N*****",
"********",
"********",
"********",
"********",
"********",
"********",
],
57
],
[
[
"********",
"********",
"**N*****",
"********",
"********",
"********",
"********",
"********",
],
55
],
[
[
"********",
"********",
"****N***",
"********",
"***N****",
"********",
"********",
"********",
],
48
],
[
[
"********",
"********",
"***N****",
"*****N**",
"**N*****",
"****N***",
"********",
"********",
],
36
],
[
[
"NNNNNNNN",
"NNN*N*NN",
"NN*NNN*N",
"NNNN*NNN",
"NN*NNN*N",
"NNN*N*NN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNNNN",
"NNN*N*NN",
"N***NN*N",
"*NNN*NNN",
"NN*NNN*N",
"*NN***NN",
"N*N*NNNN",
"NNNNNNNN",
],
2
],
[
[
"*NNNNNNN",
"NN*NNNNN",
"N*NNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNN*N",
"NNNN*NNN",
"NNNNN*N*",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNN*N*N",
"NNN*NNN*",
"NNNNN*NN",
],
1
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"*N*NNNNN",
"NNN*NNNN",
"N*NNNNNN",
"NNN*NNNN",
],
1
],
[
[
"*NNN*NNN",
"NN*NNNNN",
"*NNN*NNN",
"N*N*NNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"N*N*NNNN",
"*NNN*NNN",
"NN*NNNNN",
"*NNN*NNN",
"N*N*NNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"********",
"********",
"**N*****",
"********",
"********",
"********",
"******N*",
"N*******",
],
47
]
```
> Explanations in answers are optional, but I'm more likely to upvote answers that have one.

Given a chess board with some knights on it, say how many squares are neither attacked by a knight nor containing a knight.
## Input
- An 8 by 8 grid where each square is either a knight or empty
- You may choose to take input with any 2 distinct characters (or numbers or Booleans - there is no restriction to string input) representing a knight and an empty square
- You may take input in the format of your choice provided it does not provide additional information that would help solve the challenge
## Output
- A number from 0 to 64, indicating the number of squares that satisfy both of:
- The square does not contain a knight
- The square is not a knight's move away from a knight.
A knight's move is either of:
- 2 squares horizontally (left or right) and 1 square vertically (up or down)
- 1 square horizontally (left or right) and 2 squares vertically (up or down)
[![Knight's moves shown as dots](https://codegolf.codidact.com/uploads/Q4kXyQDf3HZiX5NWncgRS2Fi)](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "View on Wikipedia")
(thanks to [Wikipedia](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "Wikipedia section on Knight's moves"))
## Example
The following example input has knights represented by `N` and empty squares represented by `*`.
```text
********
********
**N*****
********
********
********
******N*
N*******
```
Here it is again with attacked empty squares marked as `a`. The required output is the number of remaining squares (the number of squares still showing `*`).
```text
*a*a****
a***a***
**N*****
a***a***
*a*a*a*a
*a**a***
**a***N*
N***a***
```
So for this example, the output would be `47`.
## Test cases
Test case inputs are given as 8 strings of 8 characters, followed by the output as an integer. Knights are represented by `N` and empty squares are represented by `*`.
```text
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
64
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
0
],
[
[
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
"N*N*N*N*",
"*N*N*N*N",
],
0
],
[
[
"N***N***",
"*N***N**",
"**N***N*",
"***N***N",
"N***N***",
"*N***N**",
"**N***N*",
"***N***N",
],
16
],
[
[
"N*******",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
61
],
[
[
"******N*",
"********",
"********",
"********",
"********",
"********",
"********",
"********",
],
60
],
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"********",
"*****N**",
],
59
],
[
[
"********",
"********",
"********",
"********",
"********",
"********",
"*N******",
"********",
],
59
],
[
[
"********",
"**N*****",
"********",
"********",
"********",
"********",
"********",
"********",
],
57
],
[
[
"********",
"********",
"**N*****",
"********",
"********",
"********",
"********",
"********",
],
55
],
[
[
"********",
"********",
"****N***",
"********",
"***N****",
"********",
"********",
"********",
],
48
],
[
[
"********",
"********",
"***N****",
"*****N**",
"**N*****",
"****N***",
"********",
"********",
],
36
],
[
[
"NNNNNNNN",
"NNN*N*NN",
"NN*NNN*N",
"NNNN*NNN",
"NN*NNN*N",
"NNN*N*NN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNNNN",
"NNN*N*NN",
"N***NN*N",
"*NNN*NNN",
"NN*NNN*N",
"*NN***NN",
"N*N*NNNN",
"NNNNNNNN",
],
2
],
[
[
"*NNNNNNN",
"NN*NNNNN",
"N*NNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNN*N",
"NNNN*NNN",
"NNNNN*N*",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNN*N*N",
"NNN*NNN*",
"NNNNN*NN",
],
1
],
[
[
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"*N*NNNNN",
"NNN*NNNN",
"N*NNNNNN",
"NNN*NNNN",
],
1
],
[
[
"*NNN*NNN",
"NN*NNNNN",
"*NNN*NNN",
"N*N*NNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"N*N*NNNN",
"*NNN*NNN",
"NN*NNNNN",
"*NNN*NNN",
"N*N*NNNN",
"NNNNNNNN",
"NNNNNNNN",
"NNNNNNNN",
],
1
],
[
[
"********",
"********",
"**N*****",
"********",
"********",
"********",
"******N*",
"N*******",
],
47
]
```
> Explanations in answers are optional, but I'm more likely to upvote answers that have one.

#1: Initial revision by

trichoplax‭ · 2022-09-30T21:30:04Z (about 2 years ago)

Copy Link

Raw

Markdown

Knight safe squares

Given a chess board with some knights on it, say how many squares are neither attacked by a knight nor containing a knight.

## Input
- An 8 by 8 grid where each square is either a knight or empty
- You may choose to take input with any 2 distinct characters representing a knight and an empty square
- You may take input in the format of your choice provided it does not provide additional information that would help solve the challenge

## Output
- A number from 0 to 64, indicating the number of squares that satisfy both of:
  - The square does not contain a knight
  - The square is not a knight's move away from a knight.  
A knight's move is either of:
    - 2 squares horizontally (left or right) and 1 square vertically (up or down)
    - 1 square horizontally (left or right) and 2 squares vertically (up or down)

      [![Knight's moves shown as dots](https://codegolf.codidact.com/uploads/Q4kXyQDf3HZiX5NWncgRS2Fi)](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "View on Wikipedia")  
      (thanks to [Wikipedia](https://en.wikipedia.org/wiki/Knight_(chess)#Movement "Wikipedia section on Knight's moves"))

## Example
The following example input has knights represented by `N` and empty squares represented by `*`.

```text
********
********
**N*****
********
********
********
******N*
N*******
```

Here it is again with attacked empty squares marked as `a`. The required output is the number of remaining squares (the number of squares still showing `*`).

```text
*a*a****
a***a***
**N*****
a***a***
*a*a*a*a
*a**a***
**a***N*
N***a***
```

So for this example, the output would be `47`.

## Test cases
Test case inputs are given as 8 strings of 8 characters, followed by the output as an integer. Knights are represented by `N` and empty squares are represented by `*`.

```text
[
    [
       "********",
       "********",
       "********",
       "********",
       "********",
       "********",
       "********",
       "********",
    ],
    64
],
[
    [
       "NNNNNNNN",
       "NNNNNNNN",
       "NNNNNNNN",
       "NNNNNNNN",
       "NNNNNNNN",
       "NNNNNNNN",
       "NNNNNNNN",
       "NNNNNNNN",
    ],
    0
],
[
    [
       "N*N*N*N*",
       "*N*N*N*N",
       "N*N*N*N*",
       "*N*N*N*N",
       "N*N*N*N*",
       "*N*N*N*N",
       "N*N*N*N*",
       "*N*N*N*N",
    ],
    0
],
[
    [
       "N***N***",
       "*N***N**",
       "**N***N*",
       "***N***N",
       "N***N***",
       "*N***N**",
       "**N***N*",
       "***N***N",
    ],
    16
],
[
    [
       "N*******",
       "********",
       "********",
       "********",
       "********",
       "********",
       "********",
       "********",
    ],
    61
],
[
    [
       "******N*",
       "********",
       "********",
       "********",
       "********",
       "********",
       "********",
       "********",
    ],
    60
],
[
    [
       "********",
       "********",
       "********",
       "********",
       "********",
       "********",
       "********",
       "*****N**",
    ],
    59
],
[
    [
       "********",
       "********",
       "********",
       "********",
       "********",
       "********",
       "*N******",
       "********",
    ],
    59
],
[
    [
       "********",
       "**N*****",
       "********",
       "********",
       "********",
       "********",
       "********",
       "********",
    ],
    57
],
[
    [
       "********",
       "********",
       "**N*****",
       "********",
       "********",
       "********",
       "********",
       "********",
    ],
    55
],
[
    [
       "********",
       "********",
       "****N***",
       "********",
       "***N****",
       "********",
       "********",
       "********",
    ],
    48
],
[
    [
       "********",
       "********",
       "***N****",
       "*****N**",
       "**N*****",
       "****N***",
       "********",
       "********",
    ],
    36
],
[
    [
       "NNNNNNNN",
       "NNN*N*NN",
       "NN*NNN*N",
       "NNNN*NNN",
       "NN*NNN*N",
       "NNN*N*NN",
       "NNNNNNNN",
       "NNNNNNNN",
    ],
    1
],
[
    [
       "NNNNNNNN",
       "NNN*N*NN",
       "N***NN*N",
       "*NNN*NNN",
       "NN*NNN*N",
       "*NN***NN",
       "N*N*NNNN",
       "NNNNNNNN",
    ],
    2
],
[
    [
       "*NNNNNNN",
       "NN*NNNNN",
       "N*NNNNNN",
       "NNNNNNNN",
       "NNNNNNNN",
       "NNNNNNNN",
       "NNNNNNNN",
       "NNNNNNNN",
    ],
    1
],
[
    [
       "NNNNNN*N",
       "NNNN*NNN",
       "NNNNN*N*",
       "NNNNNNNN",
       "NNNNNNNN",
       "NNNNNNNN",
       "NNNNNNNN",
       "NNNNNNNN",
    ],
    1
],
[
    [
       "NNNNNNNN",
       "NNNNNNNN",
       "NNNNNNNN",
       "NNNNNNNN",
       "NNNNNNNN",
       "NNNN*N*N",
       "NNN*NNN*",
       "NNNNN*NN",
    ],
    1
],
[
    [
       "NNNNNNNN",
       "NNNNNNNN",
       "NNNNNNNN",
       "NNNNNNNN",
       "*N*NNNNN",
       "NNN*NNNN",
       "N*NNNNNN",
       "NNN*NNNN",
    ],
    1
],
[
    [
       "*NNN*NNN",
       "NN*NNNNN",
       "*NNN*NNN",
       "N*N*NNNN",
       "NNNNNNNN",
       "NNNNNNNN",
       "NNNNNNNN",
       "NNNNNNNN",
    ],
    1
],
[
    [
       "N*N*NNNN",
       "*NNN*NNN",
       "NN*NNNNN",
       "*NNN*NNN",
       "N*N*NNNN",
       "NNNNNNNN",
       "NNNNNNNN",
       "NNNNNNNN",
    ],
    1
],
[
    [
       "********",
       "********",
       "**N*****",
       "********",
       "********",
       "********",
       "******N*",
       "N*******",
    ],
    47
]
```

> Explanations in answers are optional, but I'm more likely to upvote answers that have one.

code-golf

Communities

Post History